Четырехмерное пространство

Описание четырехмерного пространства

Из курса линейной алгебры следует, что вектор – это элемент любой природы. Поэтому в качестве вектора можно выбрать совокупность четырех чисел , где . В качестве правил сложения и умножения на число выбраны стандартные правила для векторов, заданных координатами:

Как видно, получаемые при помощи этих правил векторы, также являются совокупностью из четырех действительных чисел, поэтому также принадлежат данному пространству векторов, определенных как совокупность из четырех чисел; т.е. при помощи данных правил нельзя получить вектор не принадлежащий заданному линейному пространству.

О введении метрики в 4-х мерном пространстве.

Чтобы линейное пространство стало евклидовым, и в нем появилась возможность измерять расстояния и углы, необходимо определить в этом пространстве скалярное произведение. Оно определено стандартным образом, как это было сделано в трехмерном пространстве:

Тогда скалярный квадрат запишется в виде:

А длина вектора:

Угол между векторами.

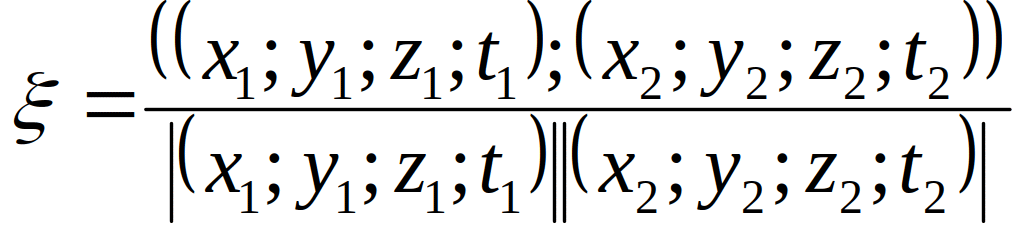Если брать векторы с различными координатами, причем одинаковой длины (вычисленной по вышеприведенной формуле), то их скалярное произведение может отличаться, поэтому существует еще один критерий, являющийся отличительной особенностью некоторого вектора по отношению к данному вектору: направленность, которая определяется углом между векторами. Пусть некоторый параметр определен следующим образом:

Как отношение скалярного произведения векторов к произведению модулей. Нетрудно видеть, что:

П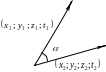 оскольку введен критерий, определяющий длину вектора, а также критерий который очевидно является угловым параметром, то вектор заданный как совокупность из 4-х чисел теперь приобретает привычный геометрический смысл. Применив правило треугольников из геометрии (при введении этого правила в школьном курсе, как известно, не оговаривается размерность пространства, а достаточно лишь знать, что вектор – это направленный отрезок) и известную теорему косинусов (размерность пространства для которой также не оговаривается, достаточно лишь знать, что треугольник – это плоская фигура, а в пространстве какой размерности он находится – безразлично), можно прийти к выводу, что , где – угол между векторами.

Линейная комбинация векторов.

П усть из линейного пространства взяты n векторов: , где , тогда выражение вида:

называется линейной комбинацией векторов (поскольку в векторам применяются линейные операции: правила сложения и умножения на число несколько раз).

Линейная зависимость и независимость векторов.

Л инейная комбинация может быть равна нулю при условии что все (это выполняется всегда). Однако может случиться так, что линейная комбинация равна нулю также при условии, что некоторый коэффициент т.е.:

Тогда:

П олучается, что мы выразили вектор через оставшиеся векторы, поэтому вектор называется линейно зависимым от остальных векторов (его всегда можно получить через остальные). Таким образом можно определить все линейно зависимые векторы и их исключить. В конечном итоге останется определенное число векторов, каждый из которых уже нельзя выразить через линейную комбинацию остальных векторов. Эти векторы называются линейно независимые.

Базис линейного пространства.

Б азис – это наибольшее количество линейно независимых векторов из данного пространства векторов.

Д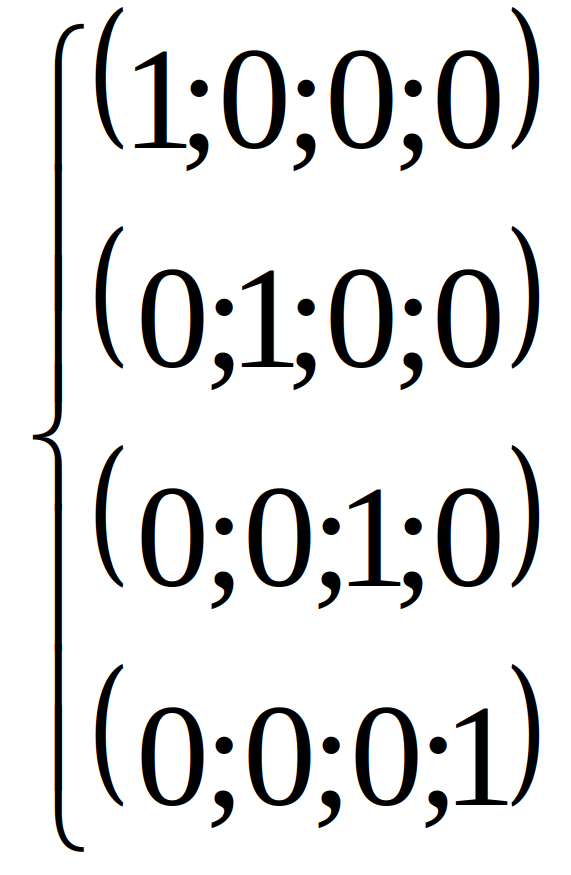 ля выбранного нами пространства векторов наибольшее число линейно независимых векторов это четыре. Базис пространства можно выбрать различными способами. Для примера выберем в качестве базиса следующие четыре вектора:

их линейная комбинация может быть записана в виде:

п оэтому:

в екторы линейно независимы, поскольку равенство нулю линейной комбинации возможно только в указанном случае.

Любой вектор можно выразить через данные векторы:

П оэтому максимальное количество линейно независимых векторов данного пространства равно четырем. Обозначим базис четырехмерного пространства следующим образом:

О длине выбранных базисных векторов.

О пределим длину при помощи ранее записанных формул:

О перпендикулярности базисных векторов.

О пределим углы между любой парой базисных векторов при помощи скалярного произведения:

О тсюда следует:

Поэтому в данном пространстве существует четыре взаимно перпендикулярных вектора.

Простейшие фигуры 4-х мерного пространства.

Простейшими фигурами в 4-х мерном пространстве (по аналогии со школьной геометрией) являются:

Точка
Прямая
Плоскость
3-х мерное пространство

Определение простейшим фигурам дать невозможно, т.к. дать определение – означает: выразить что-то через более простые понятия.

Данным фигурам можно дать лишь уточнение:

Т 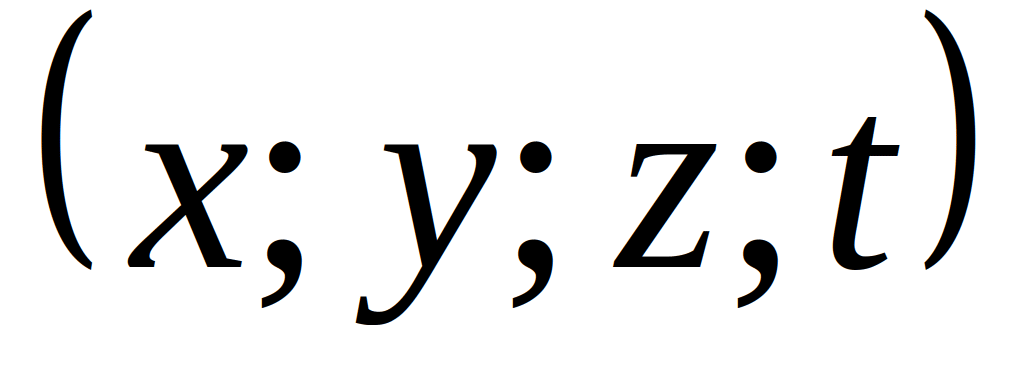очка – фигура бесконечно малых размеров (т.е. не обладающая протяженностью в пространстве). В декартовой системе координат определяется совокупностью 4-х чисел:
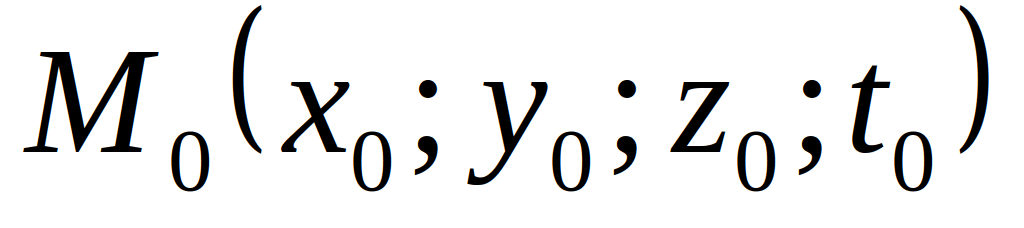
П рямая – фигура, обладающая бесконечной протяженностью по некоторому направлению. В координатном смысле это означает: множество точек, являющихся концами вектора с некоторым фиксированным началом , коллинеарного данному вектору

Т.к. условие коллинеарности – это пропорциональность координат векторов, то уравнение прямой имеет вид:

е сли направляющий вектор прямой задан как:

, то прямая имеет вид:

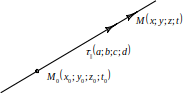
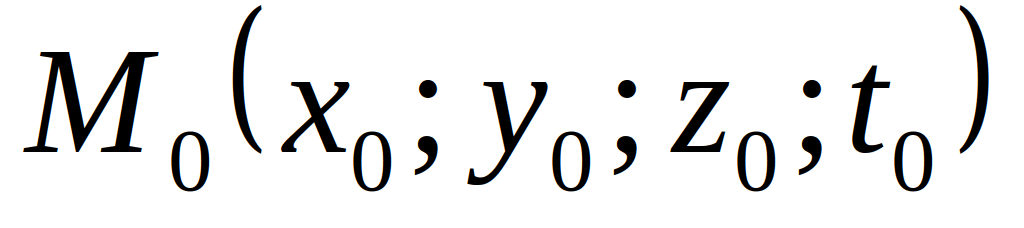
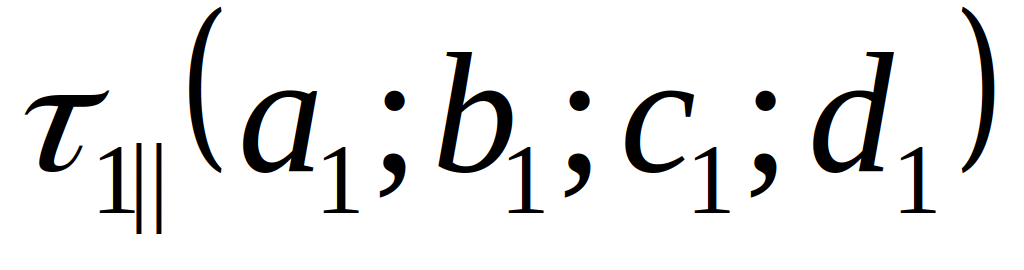
П 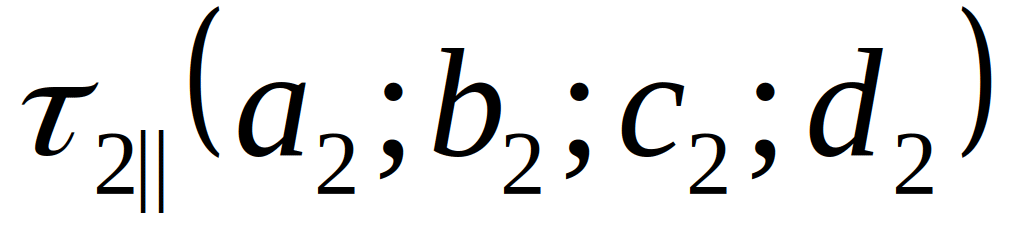лоскость – фигура, обладающая бесконечной протяженностью по двум независимым направлениям. Другими словами, это множество точек, являющихся концами вектора с некоторым фиксированным началом , компланарного двум данным независимым векторам и
П ространство – фигура, обладающая бесконечной протяженностью по трем независимым направлениям. Поскольку в 4-х мерном пространстве в любой точке можно построить четыре взаимно перпендикулярных вектора, то определению пространства удовлетворяет множество точек, являющихся концами векторов, исходящих из данной точки перпендикулярно данному вектору (нормали к пространству).

– нормаль к пространству.

– фиксированная точка пространства

– произвольная точка пространства

Тогда:

у равнение трехмерного пространства в 4-х мерном можно записать виде:

Аксиомы 4-х мерного пространства и следствия из них.

К аксиомам планиметрии и стереометрии, известных из школьного курса геометрии, следует добавить еще одну группу аксиом:

Аксиомы группы D:

К 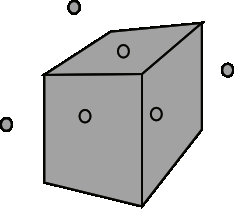аково бы ни было трехмерное пространство, существуют точки принадлежащие этому пространству и точки не принадлежащие ему
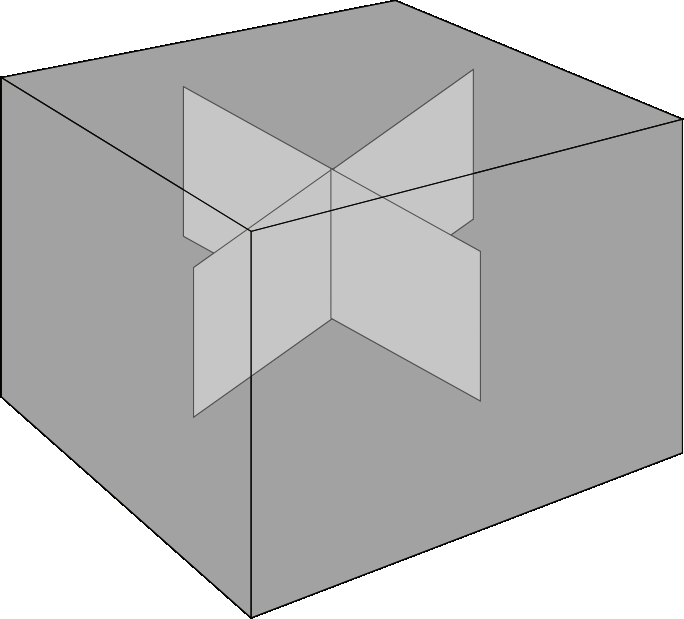
Е 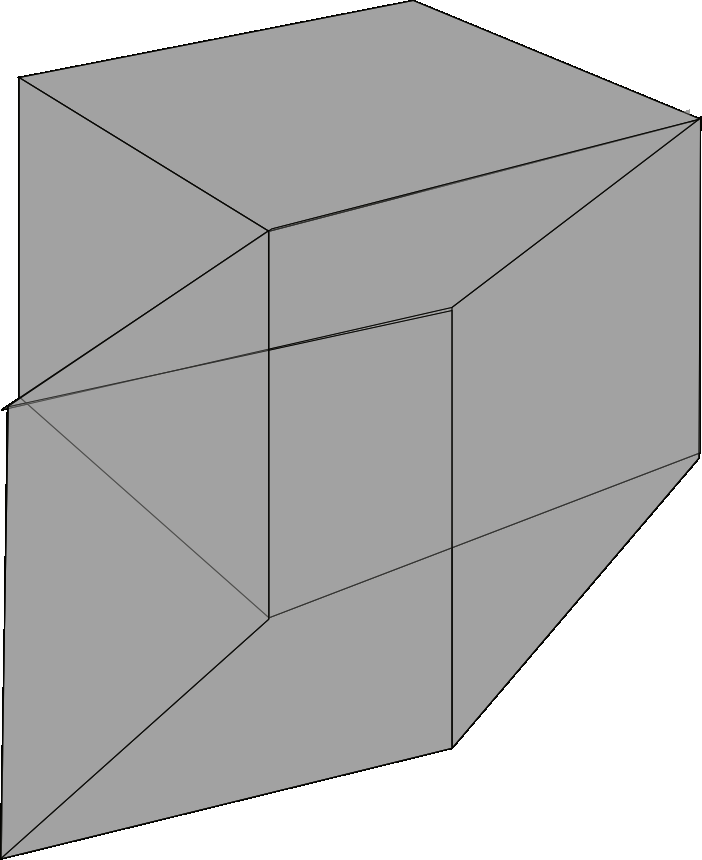сли две различные плоскости имеют общую прямую, то через них можно провести трехмерное пространство и притом только одно.
Если два различных 3-х мерных пространства имеют общую точку, то через них можно провести плоскость и притом только одну.

Некоторые определения:

Параллельными 3-х мерными пространствами называются пространства, принадлежащие одному 4-х мерному пространству и не имеющие общих точек.
Перпендикулярные 3-х мерные пространства, это пространства, пересекающиеся под прямым углом, т.е.: 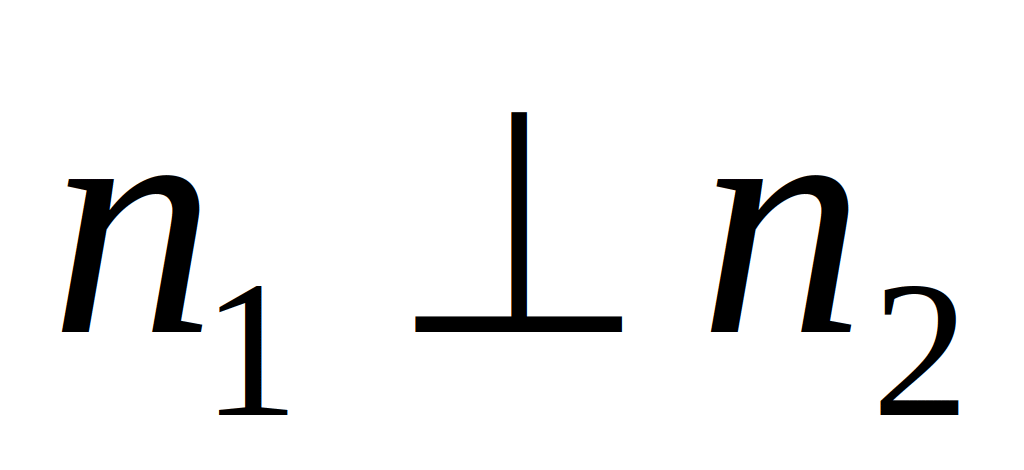(нормали перпендикулярны).
Прямая и плоскость называются параллельными, если они лежат в одном 3-х мерном пространстве и не пересекаются.
плоскости называются параллельными, если они лежат в одном 3-х мерном пространстве и не пересекаются.

Следствия из аксиом:

Через 4 точки не лежащие в одной плоскости можно провести 3-х мерное пространство и притом только одно
Через три прямые имеющие общую точку и не лежащие в одной плоскости можно провести 3-х мерное пространство и притом только одно
Через плоскость и прямую не лежащую в этой плоскости, имеющие общую точку, можно провести 3-х мерное пространство и притом только одно
Через плоскость и не лежащую на ней точку можно провести 3-х мерное пространство и притом только одно
Если две плоскости не лежат в одном пространстве, то они могут пересекаться в точке, либо не пересекаться (скрещивающиеся плоскости)
Через некоторую точку 4-х мерного пространства могут проходить четыре взаимно перпендикулярные 3-х мерные пространства

О преобразовании подобия. Гомотетия

Преобразование подобия – это геометрическое преобразование фигуры, при котором расстояние между двумя любыми точками фигуры изменяется в некоторое фиксированное количество раз, т.е. справедливо соотношение: .

Гомотетия – это преобразование, при котором любая точка пространства преобразуется в точку следующим образом: , где – центр гомотетии (некоторая фиксированная точка пространства).

Гомотетия является преобразованием подобия, т.е. отрезки преобразуются в пропорциональные отрезки и сохраняются углы между отрезками.

В настоящей работе для отображения точек четырехмерного пространства на трехмерное используется центральное проецирование: точка 4-х мерной фигуры преобразуется в точку 3-х мерной, которая является пересечением 3-х мерного пространства и прямой, проходящей через две точки 4-х мерного пространства ( и ). Таким образом все прямые проходят через общий центр проецирования – центр гомотетии. Разумеется центральная проекция не является преобразованием подобия, она позволяет снизить размерность фигуры, сохранив при этом информацию о ее особенностях (сохраняются количество отрезков и вершин фигуры), иначе 4-х мерная фигура не являлась бы полностью обозримой для трехмерного глаза (подобно тому как невозможно, используя преобразование подобия отобразить 3-х мерный куб на плоскость). При снижении размерности фигуры приходится жертвовать информацией об углах между ее ребрами, однако наблюдая фигуру в динамике человеческий мозг способен сложить объективное представление о ней.

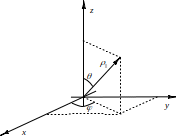
Сферическая система координат.

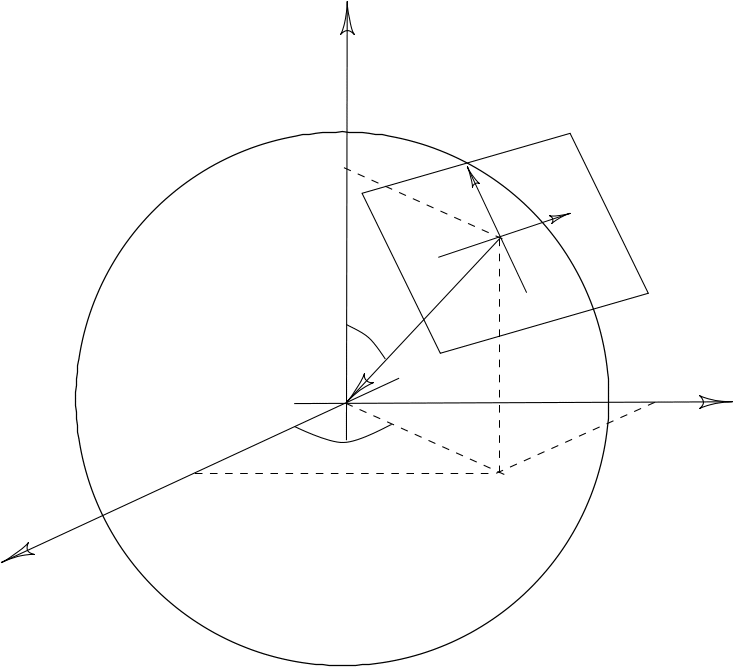
Для того чтобы спроецировать на плоскость (экрана) тень 4-х мерной фигуры (проекцию на 3-х мерное пространство), необходимо определиться с ориентацией плоскости в 3-х мерном пространстве.

Наиболее логично выбрать ее ориентацию так, чтобы нормаль к плоскости смотрела все время в начало координат (вблизи начала координат находится рассматриваемая фигура), оставаясь при этом на определенном расстоянии от него. Таким образом плоскость должна быть касательной к сфере с центром в начале координат. Наиболее просто описывать положение такой плоскости, используя сферическую систему координат. Связь между декартовой системой координат и сферической:

П усть точка касания плоскости со сферой: , тогда нормаль к плоскости можно записать в виде: . векторы и находятся в плоскости, касательной к сфере с центром в начале координат и радиусом .

Векторы и необходимо записать в таком виде, чтобы выполнялись условия взаимной перпендикулярности каждой пары векторов из рассматриваемой тройки. Запишем их в следующем виде:

Н етрудно видеть (записав скалярное произведение), что эти векторы перпендикулярны между собой, а также перпендикулярны нормали к поверхности: , причем каждый из векторов и является единичным.

П ересечение прямой с плоскостью в 3-х мерном пространстве.

Д опустим плоскость проходит через точку , тогда нормаль к плоскости можно записать в виде: , а уравнение плоскости выглядит так:

П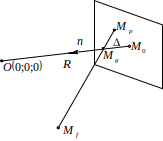 усть – расстояние от центра гомотетии до плоскости, тогда координаты центра гомотетии можно найти из условия пропорциональности длин отрезков:

тогда центр гомотетии имеет

координаты:

пересечением прямой с плоскостью является точка, удовлетворяющая системе уравнений:

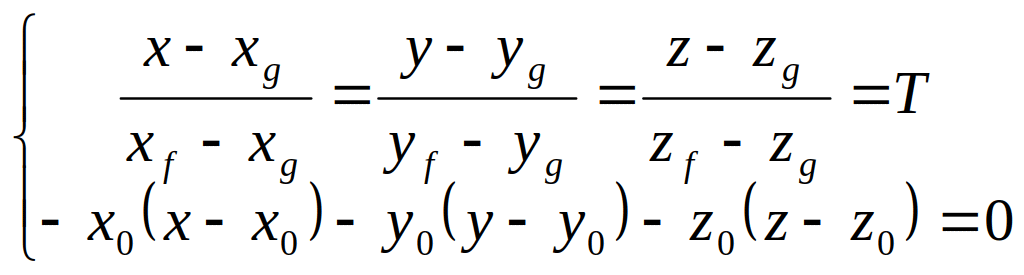
где T – некоторый параметр, а – точка проецируемой фигуры.

И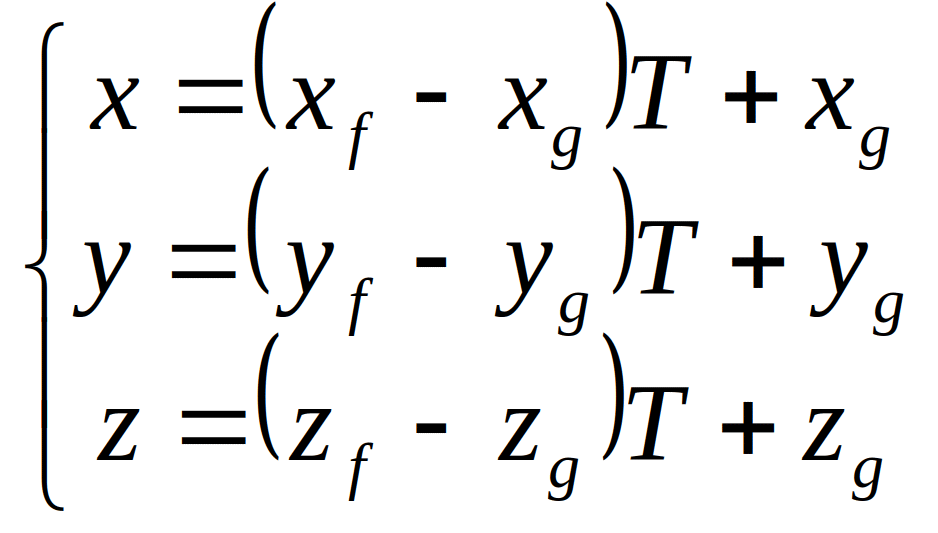 з рассматриваемой системы следует, что:

П одставляя эти значения в уравнение плоскости, найдем параметр T:

Зная параметр Т, найдем координаты проекции точки фигуры на плоскость (экрана).

Нахождение координат точки плоскости в новом базисе

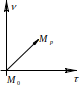
Т еперь необходимо найти координаты спроецированной точки в новом базисе, однако нас интересуют лишь проекции на оси с ортами и . для их нахождения необходимо найти скалярное произведение ортов и вектора

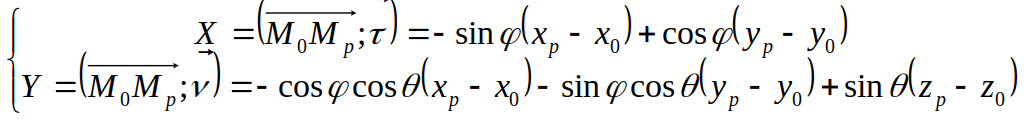И так, координаты проекции точки фигуры в системе координат, связанной с экраном:

Гиперсферическая система координат.

Д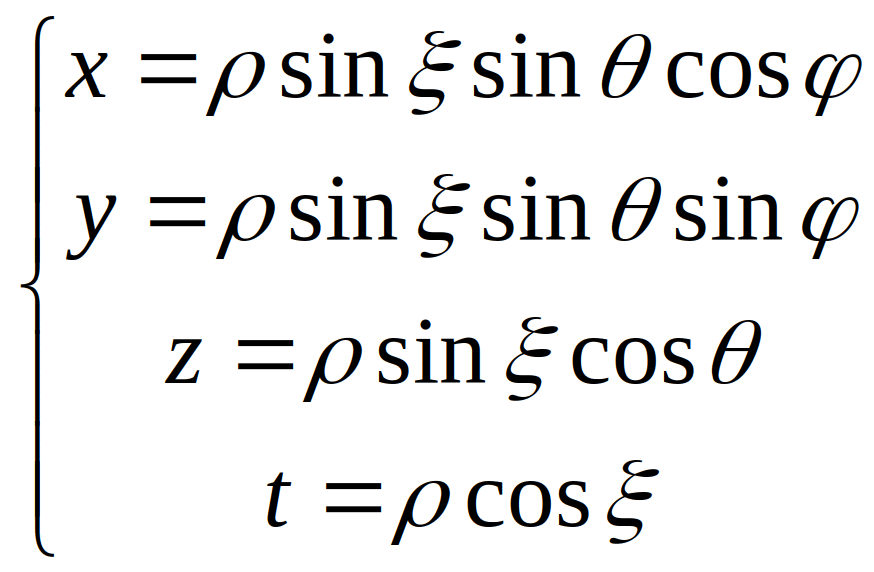 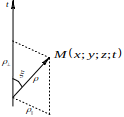ля удобства обозрения гиперфигур, будем располагать их вблизи начала координат. Наиболее самоочевидным и динамичным способом рассмотрения гиперфигур с различных сторон является вращение вокруг них по гиперсфере. В этом случае 3-х мерное пространство, касательное к гиперсфере имеет нормаль, смотрящую в начало координат (данная нормаль является лучом зрения). Для удобства построения перехода от декартовой к сферической системе координат, разобьем рисунок на две составляющие, тогда из определения тригонометрических функций автоматически следуют формулы перехода:

Если то, варьируя тремя параметрами: , мы способны переместиться в любую точку поверхности гиперсферы, т.е. способны обозревать фигуру близ начала координат с любой стороны.

Теперь необходимо спроецировать гиперфигуру на 3-х мерное пространство.

Как уже было сказано, точка обзора находится на гиперсфере радиуса и описывается формулами перехода. Пусть она является точкой касания некоторого 3-х мерного пространства с гиперсферой:

т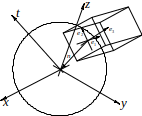 огда нормаль к 3-х мерному касательному пространству можно записать в виде: . векторы: находятся в касательном пространстве. Как и для случая сферической системы координат, эти векторы следует записать в таком виде, чтобы они были единичными и перпендикулярными между собой, а также перпендикулярные нормали к пространству (т.е. чтобы в касательном пространстве они образовывали ортонормированный базис). Запишем их в виде:

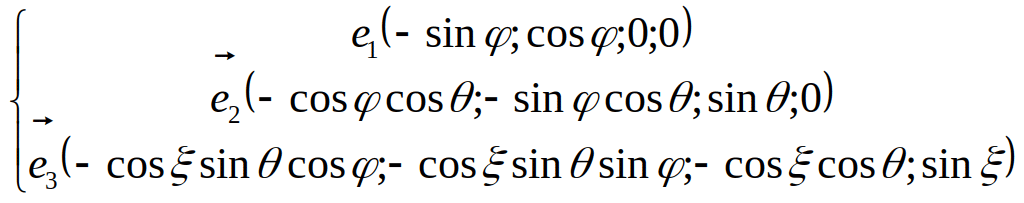
Записав скалярное произведение, нетрудно проверить, что они взаимно перпендикулярны, а также перпендикулярны нормали к касательному пространству. Таким образом, варьируя параметрами , т.е. изменяя углы обзора, мы поворачиваем касательное пространство вокруг гиперфигуры, оставляя луч зрения всегда направленным в центр 4-х мерной системы координат.

Пересечение прямой с 3-х мерным пространством в 4-х мерном пространстве.

к ак было записано ранее пространство проходит через точку гиперсферы тогда нормаль к пространству:

у равнение пространства в этом случае имеет вид:

П 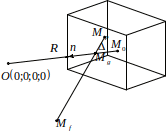усть – расстояние от центра гомотетии до касательного пространства (центр гомотетии не лежит в касательном трехмерном пространстве), тогда координаты центра гомотетии можно найти из условия пропорциональности длин отрезков:

тогда центр гомотетии имеет

координаты:

пересечением прямой с 3-х мерным пространством является точка, удовлетворяющая системе уравнений:

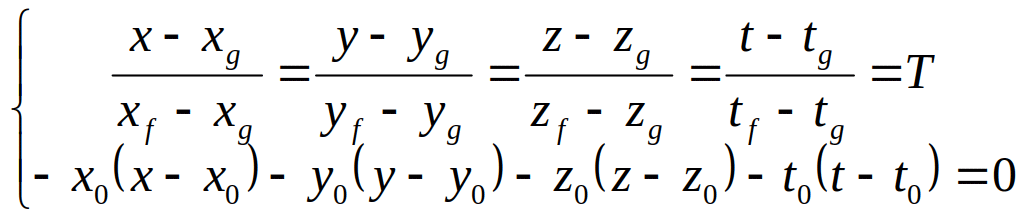
где T – некоторый параметр, а – точка проецируемой фигуры.

Из рассматриваемой системы следует, что:

Подставляя эти значения в уравнение плоскости, найдем параметр T:

Зная параметр Т, найдем координаты проекции точки фигуры на 3-х мерное пространство.

Нахождение координат точки пространства в новом базисе

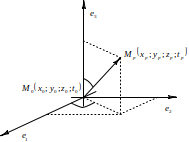
Т еперь необходимо найти координаты спроецированной точки в новом базисе, однако нас интересуют лишь проекции на оси с ортами . Для их нахождения необходимо найти скалярное произведение ортов и вектора

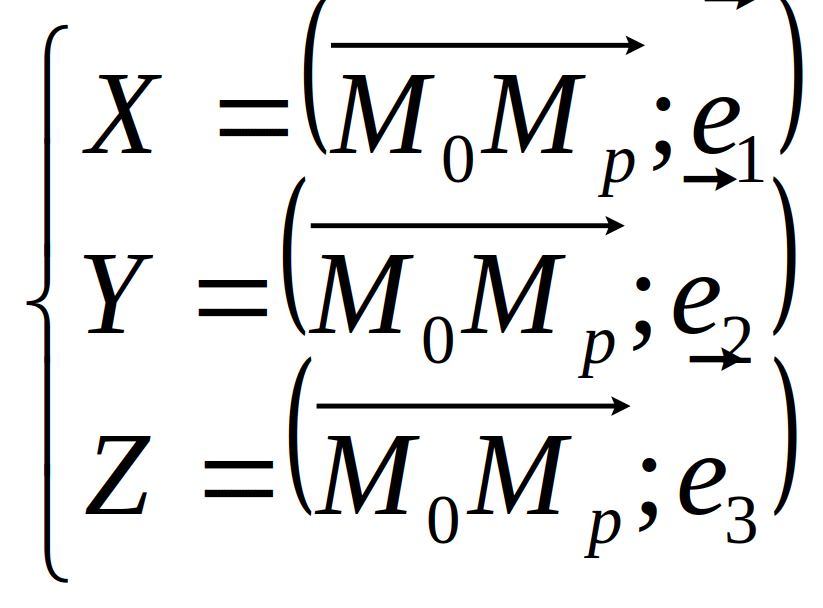И так, координаты проекции точки фигуры в системе координат, связанной с подвижным касательным пространством к гиперсфере:

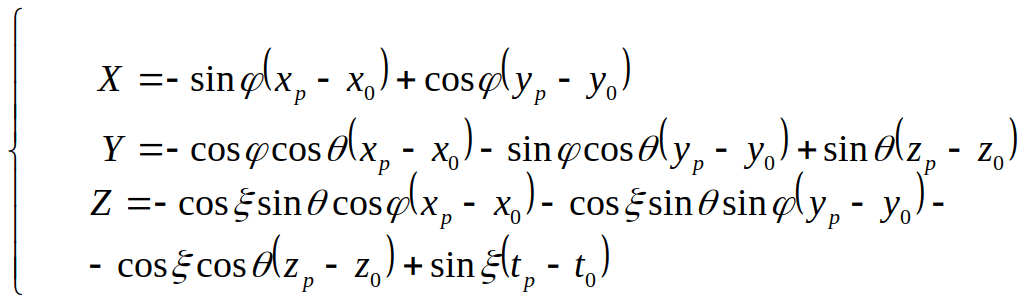
Подытожим все вышесказанное:

Описанная методика проецирования позволяет отобразить любую точку гиперфигуры на трехмерное пространство. После этого следует точку трехмерного пространства отобразить на плоскость. Реализуя данную методику программными методами – получим визуализацию гиперфигуры.

Обозримость точек плоскости из 3-х мерного пространства.

Н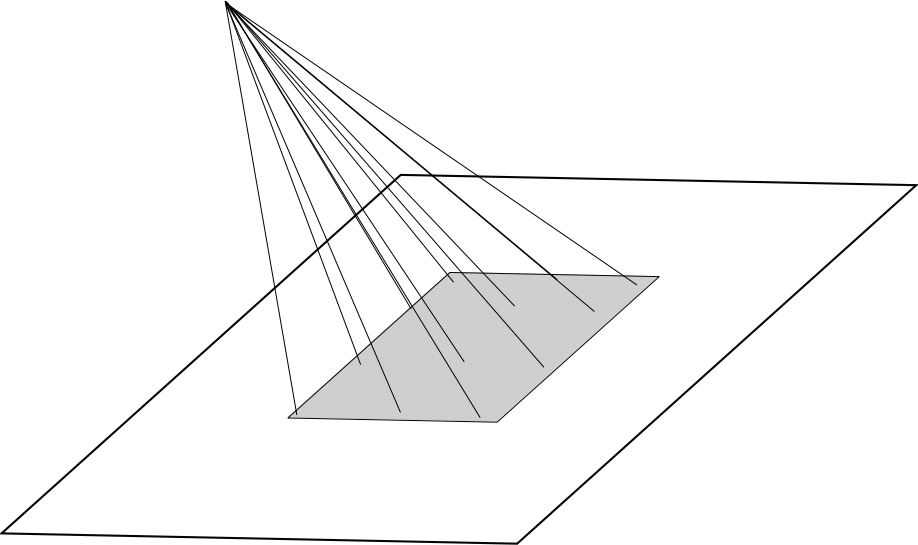 аходясь в двумерном пространстве, невозможно видеть внутреннюю часть сплошного квадрата, однако если смотреть на квадрат из точки, не лежащей с ним в одной плоскости, то можно видеть сразу все его точки. Математически это означает, что: если прямая, находящаяся в плоскости квадрата имеет с ним общую точку, то количество всех общих точек для прямой и квадрата – бесконечное. Если же прямая не принадлежит плоскости квадрата, то с этой плоскостью она может пересекаться всего лишь в одной точке.

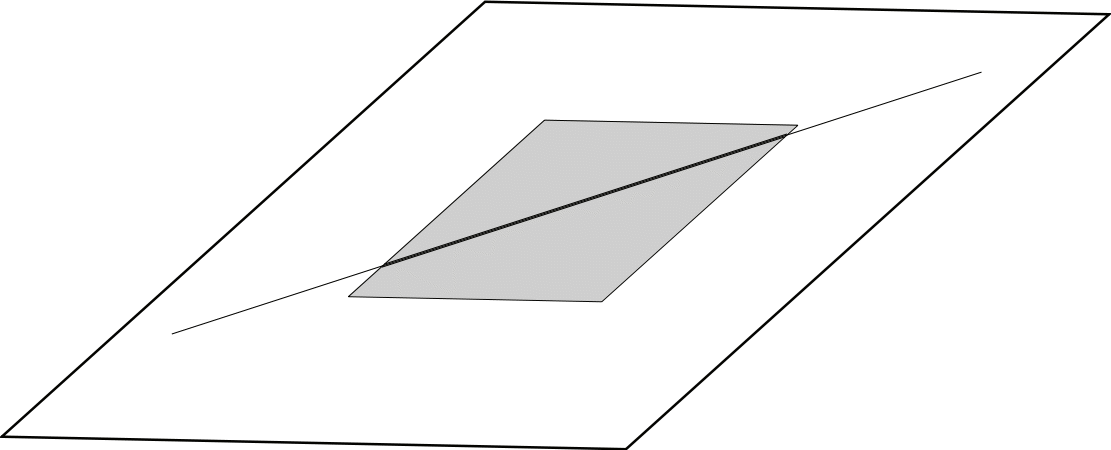
Поэтому трехмерный глаз может видеть сразу все точки квадрата.

Обозримость точек 3-х мерного пространства из 4-х мерного.

Н аходясь в 3-х мерном пространстве, невозможно видеть внутреннюю часть сплошного куба, однако если смотреть на куб из точки, не лежащей с ним в одном трехмерном пространстве, то можно видеть сразу все его точки. Математически это означает, что: если прямая, находящаяся в одном 3-х мерном пространстве с кубом, имеет с ним общую точку, то количество всех общих точек для прямой и куба – бесконечное. Если же прямая не принадлежит 3-х мерному пространству куба, то с этим 3-х мерным пространством она может пересекаться всего лишь в одной точке.

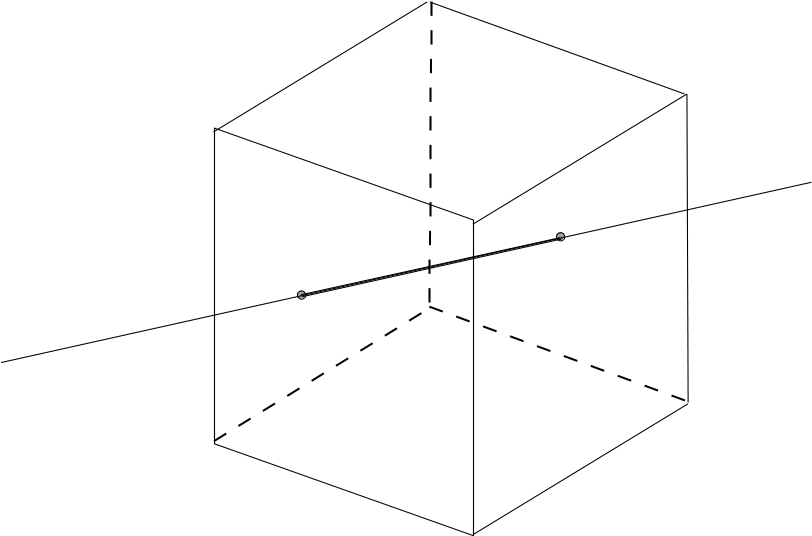
Поэтому 4-х мерный глаз может видеть сразу все точки 3-х мерного куба (всевидящее око).

О 3-х мерном и 4-х мерном глазе.

Всем известно, что 3-х мерный глаз, это система, состоящая из плоскости проецирования (сетчатки) и точки, не принадлежащей этой плоскости, являющейся центром проецирования (хрусталика).

По аналогии с 3-х мерным глазом, нетрудно представить себе как выглядит 4-х мерный глаз: это система, состоящая из 3-х мерного пространства проецирования (аналогия сетчатки) и точки, не принадлежащей этому пространству, являющейся центром проецирования (аналогия хрусталика).

Подобно тому, как хрусталик 3-х мерного глаза представляет из себя выпуклую линзу, являющуюся геометрическим местом точек пересечения двух шаров, так и хрусталик 4-х мерного глаза представляет из себя выпуклую линзу, являющуюся геометрическим местом точек пересечения гипершаров.

Вращение вокруг прямой в 3-х мерном пространстве.

В 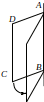3-х мерном пространстве существует бесконечное множество прямых, проходящих через некоторую точку данной прямой, перпендикулярно ей: , поэтому в 3-х мерном пространстве возможно вращение вокруг прямой. Вращение – означает изменение координат точек фигуры, находящихся вне данной прямой (оси вращения), при неизменных координатах точек фигуры на данной прямой. Квадрат ABCD вращается вокруг прямой AB, это означает, что координаты всех точек квадрата не принадлежащих AB изменяются (согласно правилу преобразования подобия), а координаты точек принадлежащих AB – не изменяются.

Вращение вокруг плоскости в 4-х мерном пространстве.

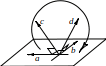
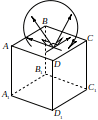В 4-х мерном пространстве существует бесконечно много прямых, проходящих через некоторую точку данной плоскости, перпендикулярно ей, потому что плоскость задана двумя ортогональными векторами. Поскольку в 4-х мерном пространстве можно построить 4-ре взаимно ортогональных вектора, исходящих из данной точки, то плоскость будет перпендикулярна любому вектору, являющемуся линейной комбинацией векторов и . Вращение вокруг рассматриваемой плоскости происходит в плоскости, образованной векторами и . Координаты любой точки квадрата при вращении куба вокруг плоскости – остаются неизменными, а координаты всех остальных точек изменяются по правилам преобразования подобия.